问题：

问题一：一个合法的表达式由()包围，()可以嵌套和连接，如(())()也是合法表达式；现在有 6 对()，可以组成的合法表达式的个数是多少？

问题二：在图书馆一共6个人在排队，3个还《面试宝典》一书，3个在借《面试宝典》一书，图书馆此时没有了面试宝典了，求他们排队的总数？

问题三：一个栈(无穷大)的进栈序列为1,2,3,..n,有多少个不同的出栈序列?

这几个都是笔试题，考察的就是catalan数，那么Catalan数是什么呢，看一下wikipedia就知道了：

卡塔兰数是组合数学中一个常在各种计数问题中出现的数列。以比利时的数学家欧仁·查理·卡塔兰（1814–1894）命名。历史上，清代数学家明安图(1692年－1763年)在其《割圜密率捷法》最早用到“卡塔兰数”，远远早于卡塔兰[1][2][3]。有中国学者建议将此数命名为“明安图数”或“明安图-卡塔兰数”[4]。

表达式：

一般项表达式：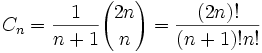

递推关系：h(n)= h(1)h(n-1) + h(2)h(n-2) + …+ h(n-1)h(1) (其中n>=2) n的catalan数为：h(n)=C(2n,n)/(n+1)，C(2n,n)表示2n的n个数的组合。又有h(n) = C(2n, n) - C(2n, n-1);

证明：

以问题一为例，我们把’(‘当成1，’)’当成0，这样就转换成了一个01串，要求为对于任一位置，其前面的1的个数不得少于0的个数。这样我们就可以把所有的组合数-不符合的组合数，就得到结果了。那不符合的情况是什么样的呢：从左向右扫描，必然会在某一奇数位是0（因为前面偶数个0和1是符合要求的），然后把这个0以后的所有0换成1，1换成0，当01总数为2n时，此时有（n+1）个1，（n-1）个0.那么，当存在上述情况时，就反证了此时存在一个不符合的情况，于是，不符合的组合数为C(2n, n-1)!所以得出： h(n) = C(2n, n) - C(2n, n-1)

结论：

不想看上边乱七八糟的，直接看结论，那就是：h(n) = C(2n, n) - C(2n, n-1)，C(2n,n)表示2n的n个数的组合。

第一次写博客，有不对的地方，欢迎指正。